MECÂNICA DECADIMENSIONAL GRACELI [NO SDCTIE GRACELI]
A MECÂNICA SDCTIE GRACELI É UM SISTEMA FUNDAMENTADO EM CINCO PILARES;
dez ou mais dimensões de graceli SISTEMA DECADIMENSIONAL GRACELI].
CATEGORIAS DE GRACELI.
ESTADOS TRANSICIONAIS E FENOMÊNICOS DE GRACELI.
TRANSFORMAÇÕES. E INTERAÇÕES.
DENTRO DO SISTEMA DE DIMENSÕES NÃO ENTRA O ESPAÇO E O TEMPO, LOGO NÃO SEGUE VARIAÇÕES CURVAS GEOMÉTRICAS, OU EM RELAÇÃO AO TEMPO, OU LATITUDE, LONGITUDE E ALTURA.
MAS SIM, DIMENSÕES DA MATÉRIA, ENERGIAS, FENÔMENOS E ESTADOS TRANSICIONAIS.
VER PUBLICADO NA INTERNET:
DIMENSÕES DE GRACELI, E DIMENSÕES DE ESTADOS TRANSICIONAIS.
NÃO SEGUE UMA RELAÇÃO DE ENERGIA E MATÉRIA,
MAS SIM DE CATEGORIAS, UM SISTEMA DECADIMENSIONAL E ESTADOS TRANSICIONAIS.
E NEM VARIAÇÕES DE MOVIMENTOS E MOMENTUM.
MAS SIM, VARIAÇÕES DE ESTRUTURAS, ESTADOS TRANSICIONAIS. CONFORME O SDCITE GRACELI.
PARA ENTENDER O SDCTIE GRACELI.
ELETRO-ENTROPIA QUÂNTICA GRACELI NO SDCTIE GRACELI
CONFORME A INTENSIDADE DE DESCARGAS ELÉTRICAS COMO RAIOS, RELÂMPAGOS, ENCONTROS DE FIOS DE ALTA TENSÃO OCORREM DESORDEM E TRANSFORMAÇÕES DE CARGAS ELÉTRICAS E ALTERAÇÕES MAGNÉTICAS COM VARIAÇÕES EXPONENCIAIS CONFORME A INTENSIDADES DAS DESCARGAS ELÉTRICAS.
E COM ALTERAÇÕES NOS ESTADOS QUÂNTICO DE CADA ÍONS, E VARIAÇÕES ALEATÓRIAS DE FLUXOS NO MEIO EM QUE SE ENCONTRAM [NO ESPAÇO OU DENTRO DOS MATERIAIS.
COM ISTO SE TEM A ELETRO-ENTROPIA GRACELI..
VEJAMOS:
A LUZ É UMA ENERGIA ELETROMAGNÉTICA NUM SISTEMA DIMENSIONAL DE ESTADOS QUÂNTICOS.
OU SEJA, NESTE CASO NÃO SE APRESENTA NEM COMO ONDA E NEM COMO PARTÍCULA.
TERCEIRA QUANTIZAÇÃO PELO SDCTIE GRACELI
TRANS-QUÂNTICA SDCTIE GRACELI, TRANSCENDENTE, RELATIVISTA SDCTIE GRACELI, E TRANS-INDETERMINADA.
FUNDAMENTA-SE EM QUE TODA FORMA DE REALIDADE SE ENCONTRA EM TRANSFORMAÇÕES, INTERAÇÕES, TRANSIÇÕES DE ESTADOS [ESTADOS DE GRACELI], ENERGIAS E FENÔMENOS DENTRO DE UM SISTEMA DE DEZ OU MAIS DIMENSÕES DE GRACELI, E CATEGORIAS DE GRACELI.
FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI
FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI. E DE ESTADOS TRANSICIONAIS =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
x
[EQUAÇÃO DE DIRAC].
+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
, + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+ FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
X
-
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......
ΤDCG
X
Δe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
x
sistema de dez dimensões de Graceli +
DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..
-
-
DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.
x
sistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].
x
número atômico, estrutura eletrônica, níveis de energia
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
- X
- CATEGORIAS DE GRACELI
-
T l T l E l Fl dfG l
X TODA E QUALQUER FORMA DE FUNÇÃO OU EQUAÇÃO =
TRANSFORMAÇÕES ⇔ INTERAÇÕES ⇔ TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔ Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS, ⇔ Δ MASSA , ⇔ Δ CAMADAS ORBITAIS , ⇔ Δ FENÔMENOS , ⇔ Δ DINÂMICAS, ⇔ Δ VALÊNCIAS, ⇔ Δ BANDAS, Δ entropia e de entalpia, E OUTROS.
[EQUAÇÃO DE DIRAC].+ FUNÇÃO TÉRMICA.
+ FUNÇÃO DE RADIOATIVIDADE
+ FUNÇÃO DE RADIOATIVIDADE
, + FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ FUNÇÃO DE TUNELAMENTO QUÂNTICO.
+ ENTROPIA REVERSÍVEL
+ ENTROPIA REVERSÍVEL + FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
![\sigma =q(n\mu _{n}+p\mu _{p})[\Omega .cm]^{{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d1173dd9d9ec55715f1f4beb1ea5dcd4932bc8)
FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA
ENERGIA DE PLANCK
ENERGIA DE PLANCK
X
V [R] [MA] = Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......ΤDCG XΔe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM...... =
xsistema de dez dimensões de Graceli +DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..- DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.xsistema de transições de estados, e estados de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].x
número atômico, estrutura eletrônica, níveis de energia
- TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
- X
- CATEGORIAS DE GRACELI
- DT l T l E l Fl dfG lN l El tf lP l Ml tfefelTa l RlLl
X TODA E QUALQUER FORMA DE FUNÇÃO OU EQUAÇÃO =
Um passeio aleatório é um objeto matemático que descreve um caminho que consiste de uma sucessão de passos aleatórios. Por exemplo, o caminho traçado por uma molécula conforme ela viaja em um líquido ou um gás, o caminho de um animal buscando alimento, comportamento de supercordas, o preço flutuante de ações e da situação financeira de um jogador pode ser aproximada por modelos de passeio aleatório, mesmo que eles possam não ser verdadeiramente aleatórios na realidade. Como ilustrado por esses exemplos, passeios aleatórios têm aplicações em muitas áreas científicas, incluindo ecologia, psicologia, ciência da computação, física, química, e biologia, e também para a economia. Os passeios aleatórios explicam os comportamentos observados em muitos processos desses campos, e, assim, serve como um modelo fundamental para o registro de atividades estocásticas. Como um aplicação matemática, o valor de pi pode ser aproximado pela utilização de passeios aleatórios no ambiente de modelagem.[1][2] O termo passeio aleatório foi introduzido pela primeira vez por Karl Pearson , em 1905.[3]
Vários tipos diferentes de passeios aleatórios são de interesse, que podem diferir em vários aspectos. O próprio termo geralmente se refere a uma categoria especial de cadeias de Markov ou processos de Markov, mas muitos processos dependentes do tempo são referidos como passeios aleatórios, com um modificador que indica suas propriedades específicas. Passeios aleatórios (de Markov ou não) também podem acontecer em uma variedade de espaços: os mais comumente estudados incluem gráficos, outros entre os números inteiros ou reais, no plano ou em espaços vetoriais de dimensões superiores, em superfícies curvas ou em dimensões superiores de campo riemaniano, e também em grupos finitos, finitamente gerados ou grupo de Lie. O parâmetro de tempo também pode ser alterado. No contexto mais simples, a caminhada é em tempo discreto, que é uma sequência de variáveis aleatórias indexadas pelos números naturais. No entanto, também é possível definir passeios aleatórios que levam seus passos em momentos aleatórios, e, nesse caso, a posição tem de ser definido para todos os tempos . Casos específicos ou limites de passeios aleatórios incluem voos de Lévy e modelos de difusão, tais como o movimento Browniano.
Passeios aleatórios são um tema fundamental na discussão de processos de Markov. O estudo matemático deles tem sido intenso. Várias propriedades, incluindo, mas não limitado a distribuições de dispersão, tempo de retorno, taxas de encontro, recorrência ou transitoriedade, foram introduzidas para quantificar o seu comportamento.
Um passeio aleatório é um objeto matemático que descreve um caminho que consiste de uma sucessão de passos aleatórios. Por exemplo, o caminho traçado por uma molécula conforme ela viaja em um líquido ou um gás, o caminho de um animal buscando alimento, comportamento de supercordas, o preço flutuante de ações e da situação financeira de um jogador pode ser aproximada por modelos de passeio aleatório, mesmo que eles possam não ser verdadeiramente aleatórios na realidade. Como ilustrado por esses exemplos, passeios aleatórios têm aplicações em muitas áreas científicas, incluindo ecologia, psicologia, ciência da computação, física, química, e biologia, e também para a economia. Os passeios aleatórios explicam os comportamentos observados em muitos processos desses campos, e, assim, serve como um modelo fundamental para o registro de atividades estocásticas. Como um aplicação matemática, o valor de pi pode ser aproximado pela utilização de passeios aleatórios no ambiente de modelagem.[1][2] O termo passeio aleatório foi introduzido pela primeira vez por Karl Pearson , em 1905.[3]
Vários tipos diferentes de passeios aleatórios são de interesse, que podem diferir em vários aspectos. O próprio termo geralmente se refere a uma categoria especial de cadeias de Markov ou processos de Markov, mas muitos processos dependentes do tempo são referidos como passeios aleatórios, com um modificador que indica suas propriedades específicas. Passeios aleatórios (de Markov ou não) também podem acontecer em uma variedade de espaços: os mais comumente estudados incluem gráficos, outros entre os números inteiros ou reais, no plano ou em espaços vetoriais de dimensões superiores, em superfícies curvas ou em dimensões superiores de campo riemaniano, e também em grupos finitos, finitamente gerados ou grupo de Lie. O parâmetro de tempo também pode ser alterado. No contexto mais simples, a caminhada é em tempo discreto, que é uma sequência de variáveis aleatórias indexadas pelos números naturais. No entanto, também é possível definir passeios aleatórios que levam seus passos em momentos aleatórios, e, nesse caso, a posição tem de ser definido para todos os tempos . Casos específicos ou limites de passeios aleatórios incluem voos de Lévy e modelos de difusão, tais como o movimento Browniano.
Passeios aleatórios são um tema fundamental na discussão de processos de Markov. O estudo matemático deles tem sido intenso. Várias propriedades, incluindo, mas não limitado a distribuições de dispersão, tempo de retorno, taxas de encontro, recorrência ou transitoriedade, foram introduzidas para quantificar o seu comportamento.
Índice
Definição[editar | editar código-fonte]
O passeio aleatório mais simples é um caminho construído de acordo as seguintes regras:
- Há um ponto de partida.
- A distância de um ponto no caminho até o próximo é constante.
- A direção de um ponto no caminho para o próximo é escolhido aleatoriamente, e nenhuma direção é mais provável do que outra.
O passeio aleatório mais simples é um caminho construído de acordo as seguintes regras:
- Há um ponto de partida.
- A distância de um ponto no caminho até o próximo é constante.
- A direção de um ponto no caminho para o próximo é escolhido aleatoriamente, e nenhuma direção é mais provável do que outra.
Passeio aleatório em malha[editar | editar código-fonte]
Um modelo de passeio aleatório popular é o passeio aleatório em uma estrutura regular, onde a cada passo a localização salta para outro local de acordo com alguma distribuição de probabilidade. Em um passeio aleatório simples, a localização só pode saltar para locais vizinhos da rede, formando um caminho de rede. No passeio aleatório simétrico simples em uma rede localmente finita, as probabilidades do salto de localização para cada um de seus vizinhos imediatos são as mesmas. O melhor exemplo estudado é de passeio aleatório sobre o inteiro rede d-dimensional (às vezes chamado de treliça hipercúbica) .[4]
Um modelo de passeio aleatório popular é o passeio aleatório em uma estrutura regular, onde a cada passo a localização salta para outro local de acordo com alguma distribuição de probabilidade. Em um passeio aleatório simples, a localização só pode saltar para locais vizinhos da rede, formando um caminho de rede. No passeio aleatório simétrico simples em uma rede localmente finita, as probabilidades do salto de localização para cada um de seus vizinhos imediatos são as mesmas. O melhor exemplo estudado é de passeio aleatório sobre o inteiro rede d-dimensional (às vezes chamado de treliça hipercúbica) .[4]
Passeio aleatório unidimensional[editar | editar código-fonte]
Um exemplo elementar de um passeio aleatório é o passeio aleatório na linha de número inteiro, , que começa em 0 e em cada etapa move +1 ou -1 com igual probabilidade.
Este percurso pode ser ilustrado como se segue. Um marcador é colocado no zero na linha de número e uma moeda honesta é lançada. Se der cara, o marcador é movido uma unidade para a direita. Se der coroa, o marcador é movido uma unidade para a esquerda. Após cinco jogos, o marcador pode agora estar em 1, -1, 3, -3, 5, ou -5. Com cinco lançamentos, três caras e duas coroas, em qualquer ordem, vai terminar em 1. Há 10 maneiras de resultar em 1 (lançando três caras e duas coroas), 10 maneiras de resultar em -1 (lançando três coroas e duas caras), 5 formas de resultar em 3 (lançando quatro caras e uma coroa), 5 formas de resultar em -3 (lançando quatro coroas e uma cara), uma forma de resultar em 5 (lançando cinco caras), e uma forma de resultar em -5 (lançando cinco coroas). Veja abaixo uma ilustração dos resultados possíveis de 5 lançamentos.
Para definir esta caminhada formalmente, toma-se variáveis aleatórias independentes , onde cada variável é +1 ou −1, com uma probabilidade de 50% para qualquer valor, e definir e . A série é chamada passeio aleatório simples em . Esta série (a soma da seqüência de −1 e +1) dá a distância percorrida, se cada parte do passeio é de comprimento 1. A expectativa de é zero. Isto é, a média de todos os lançamentos se aproxima de zero conforme o número de lançamentos aumenta. Isto segue pela propriedade da aditividade finita da expectativa:
Um cálculo semelhante, utilizando a independência de variáveis aleatórias e o fato de que , mostra que:
Este resultado mostra que a difusão é ineficaz para a mistura devido à forma como a raiz quadrada funciona para grandes .
Quantas vezes um passeio aleatório atravessa uma linha de fronteira se for permitido continuar a caminhar para sempre? Um passeio aleatório simples em vai atravessar cada ponto um número infinito de vezes. Este resultado tem muitos nomes: o fenômeno da passagem de nível, recorrência ou o ruína do jogador. A razão para o último nome é o seguinte: um jogador com uma quantidade finita de dinheiro vai eventualmente perder ao jogar um jogo justo contra uma banca com uma quantidade infinita de dinheiro. O dinheiro do jogador irá realizar um passeio aleatório, e ele vai chegar a zero em algum ponto, e o jogo irá acabar.
Se a e b são números inteiros positivos, então o número esperado de passos até que um passeio aleatório unidimensional simples começando em 0 primeiro atingir b ou −a é ab. A probabilidade de que este passeio vai atingir b antes de −a é que pode ser derivado do fato de que o passeio aleatório simples é um martingale.
Alguns dos resultados mencionados acima podem ser derivados a partir de propriedades do triângulo de Pascal. O número de diferentes passeios de n passos, onde cada passo é +1 ou −1 é 2n. Para um passeio aleatório simples, cada um desses passeios são igualmente prováveis. Para que Sn ser igual a um número k , é necessário e suficiente que o número de passos +1 no passeio exceda o de −1 por k. O número de passeios que satisfazem é igual ao número de maneiras de escolher (n - k)/2, com n sendo o número de movimentos permitidos,[6] denotado . Para que isto tenha sentido, é necessário que n e k sejam números pares. Portanto, a probabilidade de que é igual a . Representando as entradas do triângulo de Pascal, em termos de fatoriais e usando a fórmula de Stirling, pode-se obter boas estimativas para estas probabilidades para valores grandes de .
Se o espaço é limitado para + para ser breve, o número de maneiras em que um passeio aleatório vai pousar em qualquer determinado número tendo ocorrido cinco lançamentos, pode ser mostrado como {0,5,0,4,0,1}.
Esta relação com o triângulo de Pascal é demonstrada para valores pequenos de n. Com zero lançamentos, a única possibilidade será a de permanecer em zero. No entanto, com um lançamento, há uma chance de resultar em −1, ou uma chance de resultar em 1. Com dois lançamentos, um marcador em 1 pode mover para 2 ou voltar para zero. Um marcador em −1, poderia mover para −2 ou de volta a zero. Portanto, há uma chance de resultar em −2, duas chances de terminar em zero, e uma chance de pouso em 2.
k −5 −4 −3 −2 −1 0 1 2 3 4 5 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1
O teorema do limite central e a lei do logaritmo iterado descreve aspectos importantes do comportamento de passeios aleatórios simples em . Em particular, o primeiro implica que conforme n aumenta, as probabilidades (proporcional aos números em cada linha) se aproximam de uma distribuição normal.
Um exemplo elementar de um passeio aleatório é o passeio aleatório na linha de número inteiro, , que começa em 0 e em cada etapa move +1 ou -1 com igual probabilidade.
Este percurso pode ser ilustrado como se segue. Um marcador é colocado no zero na linha de número e uma moeda honesta é lançada. Se der cara, o marcador é movido uma unidade para a direita. Se der coroa, o marcador é movido uma unidade para a esquerda. Após cinco jogos, o marcador pode agora estar em 1, -1, 3, -3, 5, ou -5. Com cinco lançamentos, três caras e duas coroas, em qualquer ordem, vai terminar em 1. Há 10 maneiras de resultar em 1 (lançando três caras e duas coroas), 10 maneiras de resultar em -1 (lançando três coroas e duas caras), 5 formas de resultar em 3 (lançando quatro caras e uma coroa), 5 formas de resultar em -3 (lançando quatro coroas e uma cara), uma forma de resultar em 5 (lançando cinco caras), e uma forma de resultar em -5 (lançando cinco coroas). Veja abaixo uma ilustração dos resultados possíveis de 5 lançamentos.
Para definir esta caminhada formalmente, toma-se variáveis aleatórias independentes , onde cada variável é +1 ou −1, com uma probabilidade de 50% para qualquer valor, e definir e . A série é chamada passeio aleatório simples em . Esta série (a soma da seqüência de −1 e +1) dá a distância percorrida, se cada parte do passeio é de comprimento 1. A expectativa de é zero. Isto é, a média de todos os lançamentos se aproxima de zero conforme o número de lançamentos aumenta. Isto segue pela propriedade da aditividade finita da expectativa:
Um cálculo semelhante, utilizando a independência de variáveis aleatórias e o fato de que , mostra que:
Este resultado mostra que a difusão é ineficaz para a mistura devido à forma como a raiz quadrada funciona para grandes .
Quantas vezes um passeio aleatório atravessa uma linha de fronteira se for permitido continuar a caminhar para sempre? Um passeio aleatório simples em vai atravessar cada ponto um número infinito de vezes. Este resultado tem muitos nomes: o fenômeno da passagem de nível, recorrência ou o ruína do jogador. A razão para o último nome é o seguinte: um jogador com uma quantidade finita de dinheiro vai eventualmente perder ao jogar um jogo justo contra uma banca com uma quantidade infinita de dinheiro. O dinheiro do jogador irá realizar um passeio aleatório, e ele vai chegar a zero em algum ponto, e o jogo irá acabar.
Se a e b são números inteiros positivos, então o número esperado de passos até que um passeio aleatório unidimensional simples começando em 0 primeiro atingir b ou −a é ab. A probabilidade de que este passeio vai atingir b antes de −a é que pode ser derivado do fato de que o passeio aleatório simples é um martingale.
Alguns dos resultados mencionados acima podem ser derivados a partir de propriedades do triângulo de Pascal. O número de diferentes passeios de n passos, onde cada passo é +1 ou −1 é 2n. Para um passeio aleatório simples, cada um desses passeios são igualmente prováveis. Para que Sn ser igual a um número k , é necessário e suficiente que o número de passos +1 no passeio exceda o de −1 por k. O número de passeios que satisfazem é igual ao número de maneiras de escolher (n - k)/2, com n sendo o número de movimentos permitidos,[6] denotado . Para que isto tenha sentido, é necessário que n e k sejam números pares. Portanto, a probabilidade de que é igual a . Representando as entradas do triângulo de Pascal, em termos de fatoriais e usando a fórmula de Stirling, pode-se obter boas estimativas para estas probabilidades para valores grandes de .
Se o espaço é limitado para + para ser breve, o número de maneiras em que um passeio aleatório vai pousar em qualquer determinado número tendo ocorrido cinco lançamentos, pode ser mostrado como {0,5,0,4,0,1}.
Esta relação com o triângulo de Pascal é demonstrada para valores pequenos de n. Com zero lançamentos, a única possibilidade será a de permanecer em zero. No entanto, com um lançamento, há uma chance de resultar em −1, ou uma chance de resultar em 1. Com dois lançamentos, um marcador em 1 pode mover para 2 ou voltar para zero. Um marcador em −1, poderia mover para −2 ou de volta a zero. Portanto, há uma chance de resultar em −2, duas chances de terminar em zero, e uma chance de pouso em 2.
| k | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||||
| 1 | 1 | ||||||||||
| 1 | 2 | 1 | |||||||||
| 1 | 3 | 3 | 1 | ||||||||
| 1 | 4 | 6 | 4 | 1 | |||||||
| 1 | 5 | 10 | 10 | 5 | 1 |
![{\displaystyle P[S_{0}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4fec1fd8784c3de7c8b113f7ff728db75c8f584)
![{\displaystyle 2P[S_{1}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c61317a7c5e847ee2756e0a746abee7bdd9da12)
![{\displaystyle 2^{2}P[S_{2}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca9583c3e61f6b6739502821af6cb79fae46f22e)
![{\displaystyle 2^{3}P[S_{3}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/283a77c450ba9f63e54a01a94fb9cec8e8ee07b8)
![{\displaystyle 2^{4}P[S_{4}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/208950bbe9ff3b0dd09b94b35dd390d3ddefea15)
![{\displaystyle 2^{5}P[S_{5}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b86e6675acd3df11dbd6fd80d3e1c0b10e3b6bf)
O teorema do limite central e a lei do logaritmo iterado descreve aspectos importantes do comportamento de passeios aleatórios simples em . Em particular, o primeiro implica que conforme n aumenta, as probabilidades (proporcional aos números em cada linha) se aproximam de uma distribuição normal.
Cadeia de Markov[editar | editar código-fonte]
Um passeio aleatório unidimensional também pode ser visto como uma cadeia de Markov cujo espaço de estado é dado por números inteiros . Para algum número p satisfazendo , as probabilidades de transição (a probabilidade Pi,j de ocorrer um movimento a partir do estado i para o estado j) são dadas por .
Um passeio aleatório unidimensional também pode ser visto como uma cadeia de Markov cujo espaço de estado é dado por números inteiros . Para algum número p satisfazendo , as probabilidades de transição (a probabilidade Pi,j de ocorrer um movimento a partir do estado i para o estado j) são dadas por .
Dimensões superiores[editar | editar código-fonte]
Em dimensões superiores, o conjunto de pontos caminhados aleatoriamente tem interessantes propriedades geométricas. Na verdade, obtém-se um fractal discreto, isto é, um conjunto que apresenta autossimilaridade estocástica em grandes escalas. Em escalas pequenas, pode-se observar a "irregularidade" resultante da grade em que o caminho é realizado. A trajetória de um passeio aleatório é o conjunto dos pontos visitados, considerado como um todo e ignorando quando o passeio chegou a cada ponto. Em uma dimensão, a trajetória é simplesmente todos os pontos entre a altura mínima e máxima que o caminho alcançou (ambos são, em média, na ordem de √n).
Para visualizar os casos de duas dimensões, pode-se imaginar uma pessoa andando aleatoriamente em torno de uma cidade. A cidade é efetivamente infinita e com calçadas dispostas em uma grade quadrada. Em cada cruzamento, a pessoa escolhe aleatoriamente uma das quatro rotas possíveis (incluindo a rota pela qual veio até aquele ponto). Formalmente, este é um passeio aleatório no conjunto de todos os pontos do plano com coordenadas nos inteiros.
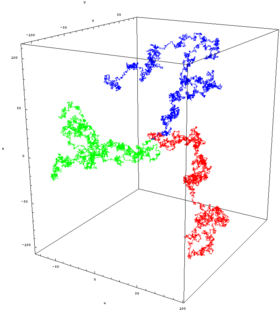
Será que a pessoa voltará em algum momento ao ponto de partida original do passeio? Este é o equivalente bidimensional da passagem de nível, discutida acima. A pessoa quase certamente irá voltar ao ponto de partida em um passeio aleatório bidimensional, mas para 3 dimensões ou mais, a probabilidade de retorno à origem diminui à medida que o número de dimensões aumenta. Em 3 dimensões, a probabilidade diminui para cerca de 34%.[9]
Em dimensões superiores, o conjunto de pontos caminhados aleatoriamente tem interessantes propriedades geométricas. Na verdade, obtém-se um fractal discreto, isto é, um conjunto que apresenta autossimilaridade estocástica em grandes escalas. Em escalas pequenas, pode-se observar a "irregularidade" resultante da grade em que o caminho é realizado. A trajetória de um passeio aleatório é o conjunto dos pontos visitados, considerado como um todo e ignorando quando o passeio chegou a cada ponto. Em uma dimensão, a trajetória é simplesmente todos os pontos entre a altura mínima e máxima que o caminho alcançou (ambos são, em média, na ordem de √n).
Para visualizar os casos de duas dimensões, pode-se imaginar uma pessoa andando aleatoriamente em torno de uma cidade. A cidade é efetivamente infinita e com calçadas dispostas em uma grade quadrada. Em cada cruzamento, a pessoa escolhe aleatoriamente uma das quatro rotas possíveis (incluindo a rota pela qual veio até aquele ponto). Formalmente, este é um passeio aleatório no conjunto de todos os pontos do plano com coordenadas nos inteiros.
Será que a pessoa voltará em algum momento ao ponto de partida original do passeio? Este é o equivalente bidimensional da passagem de nível, discutida acima. A pessoa quase certamente irá voltar ao ponto de partida em um passeio aleatório bidimensional, mas para 3 dimensões ou mais, a probabilidade de retorno à origem diminui à medida que o número de dimensões aumenta. Em 3 dimensões, a probabilidade diminui para cerca de 34%.[9]
Processo de Wiener[editar | editar código-fonte]
Um processo de Wiener é um processo estocástico com comportamento semelhante ao movimento Browniano, o fenômeno físico de partículas minúsculas difundindo em um fluido (às vezes, o processo de Wiener é chamado de "movimento Browniano", embora esse seja, estritamente falando, uma confusão de um modelo com o fenômeno a ser modelado).
Um processo de Wiener é a escala limite de passeio aleatório em uma dimensão. Isso significa que, se você tomar um passeio aleatório com passos muito pequenos, você obtém uma aproximação para um processo de Wiener (e, menos precisamente, para um movimento Browniano). Para ser mais preciso, se o tamanho do passo é ε, é preciso ter uma caminhada de comprimento L/ε2 para se aproximar de um Wiener de comprimento L. Conforme o tamanho do passo tende a 0 (e o número de passos aumenta proporcionalmente), os passeios aleatórios convergem para um processo de Wiener. Formalmente, se B é o espaço de todos os caminhos de comprimento L , com a topologia máxima, e se M é o espaço de medida através de B com a topologia normal, então a convergência se dá no espaço M. Da mesma forma, um processo de Wiener em várias dimensões é a escala limite de passeios aleatórios no mesmo número de dimensões.
Um passeio aleatório é um fractal discreto (uma função com número inteiro dimensões; 1, 2, ...), mas a trajetória de um processo de Wiener é um verdadeiro fractal, e há uma conexão entre os dois. Por exemplo, tome um passeio aleatório até que ele atinja um círculo de raio r vezes o comprimento do passo. A média do número de passos que ele executa é r2. Essa é a versão discreta do caminho de um processo de Wiener ser um fractal de dimensão Hausdorff 2.
Em duas dimensões, o número médio de pontos que o mesmo passeio aleatório tem no limite de sua trajetória é de r4/3. Isto corresponde ao fato de que o limite da trajetória de um processo de Wiener é um fractal de dimensão 4/3, um fato previsto por Mandelbrot usando simulações, mas provado apenas em 2000 por Lawler, Schramm e Werner.[10]
Um processo de Wiener possui muitas simetrias que passeio aleatório não tem. Por exemplo, um passeio em processo de Wiener é invariante à rotação, mas o passeio aleatório não, pois a grade subjacente não é invariante (passeios aleatórios são invariantes para as rotações de 90 graus, mas processos de Wiener são invariantes para rotações, por exemplo, de 17 graus). Isso significa que, em muitos casos, problemas de passeio aleatório são mais fáceis de resolver "traduzindo-os" para um processo de Wiener, resolvendo o problema e, em seguida, transformando de volta. Por outro lado, alguns problemas são mais fáceis de resolver com passeios aleatórios, devido à sua natureza discreta.
Passeios aleatórios e processos de Wiener podem ser acoplados, se manifestando sobre o mesmo espaço de probabilidade de forma dependente que os obriga a estar muito próximos. O mais simples de tais acoplamento é o acoplamento de Skorokhod, mas existem acoplamentos mais precisos, tais como o teorema de aproximação de Komlós–Grande–Tusnády.
A convergência de um passeio aleatório em direção a um processo de Wiener é controlada pelo teorema central do limite, e pelo teorema de Donsker. Para uma partícula em uma conhecida posição fixa em t = 0, o teorema central do limite diz que depois de um grande número de passos independentes no passeio aleatório, a posição do caminhante é distribuída de acordo com uma distribuição normal do total de variância:
onde t é o tempo decorrido desde o início do passeio aleatório, é o tamanho de um passo do passeio aleatório, e é o tempo decorrido entre dois passos sucessivos.
Isso corresponde à função de Green da equação de difusão que controla o processo de Wiener, o que sugere que, depois de um grande número de passos, o passeio aleatório converge em direção a um processo de Wiener.
Em 3D, a variância correspondente à função de Green de difusão da equação é:
Ao equalizar essa quantidade com a variância associada à posição do caminhante aleatório, obtém-se o coeficiente de difusão equivalente a ser considerado para o processo de Wiener para qual o passeio aleatório converge depois de um grande número de passos:
- (válido apenas em 3D)
Observação: as duas expressões da variância acima correspondem à distribuição associada ao vetor que liga as duas extremidades do passeio aleatório, em 3D. A variância associada a cada componente , ou é apenas um terço deste valor (em 3D).
Para 2D:[11]
E para 1D:[12]
Um processo de Wiener é um processo estocástico com comportamento semelhante ao movimento Browniano, o fenômeno físico de partículas minúsculas difundindo em um fluido (às vezes, o processo de Wiener é chamado de "movimento Browniano", embora esse seja, estritamente falando, uma confusão de um modelo com o fenômeno a ser modelado).
Um processo de Wiener é a escala limite de passeio aleatório em uma dimensão. Isso significa que, se você tomar um passeio aleatório com passos muito pequenos, você obtém uma aproximação para um processo de Wiener (e, menos precisamente, para um movimento Browniano). Para ser mais preciso, se o tamanho do passo é ε, é preciso ter uma caminhada de comprimento L/ε2 para se aproximar de um Wiener de comprimento L. Conforme o tamanho do passo tende a 0 (e o número de passos aumenta proporcionalmente), os passeios aleatórios convergem para um processo de Wiener. Formalmente, se B é o espaço de todos os caminhos de comprimento L , com a topologia máxima, e se M é o espaço de medida através de B com a topologia normal, então a convergência se dá no espaço M. Da mesma forma, um processo de Wiener em várias dimensões é a escala limite de passeios aleatórios no mesmo número de dimensões.
Um passeio aleatório é um fractal discreto (uma função com número inteiro dimensões; 1, 2, ...), mas a trajetória de um processo de Wiener é um verdadeiro fractal, e há uma conexão entre os dois. Por exemplo, tome um passeio aleatório até que ele atinja um círculo de raio r vezes o comprimento do passo. A média do número de passos que ele executa é r2. Essa é a versão discreta do caminho de um processo de Wiener ser um fractal de dimensão Hausdorff 2.
Em duas dimensões, o número médio de pontos que o mesmo passeio aleatório tem no limite de sua trajetória é de r4/3. Isto corresponde ao fato de que o limite da trajetória de um processo de Wiener é um fractal de dimensão 4/3, um fato previsto por Mandelbrot usando simulações, mas provado apenas em 2000 por Lawler, Schramm e Werner.[10]
Um processo de Wiener possui muitas simetrias que passeio aleatório não tem. Por exemplo, um passeio em processo de Wiener é invariante à rotação, mas o passeio aleatório não, pois a grade subjacente não é invariante (passeios aleatórios são invariantes para as rotações de 90 graus, mas processos de Wiener são invariantes para rotações, por exemplo, de 17 graus). Isso significa que, em muitos casos, problemas de passeio aleatório são mais fáceis de resolver "traduzindo-os" para um processo de Wiener, resolvendo o problema e, em seguida, transformando de volta. Por outro lado, alguns problemas são mais fáceis de resolver com passeios aleatórios, devido à sua natureza discreta.
Passeios aleatórios e processos de Wiener podem ser acoplados, se manifestando sobre o mesmo espaço de probabilidade de forma dependente que os obriga a estar muito próximos. O mais simples de tais acoplamento é o acoplamento de Skorokhod, mas existem acoplamentos mais precisos, tais como o teorema de aproximação de Komlós–Grande–Tusnády.
A convergência de um passeio aleatório em direção a um processo de Wiener é controlada pelo teorema central do limite, e pelo teorema de Donsker. Para uma partícula em uma conhecida posição fixa em t = 0, o teorema central do limite diz que depois de um grande número de passos independentes no passeio aleatório, a posição do caminhante é distribuída de acordo com uma distribuição normal do total de variância:
onde t é o tempo decorrido desde o início do passeio aleatório, é o tamanho de um passo do passeio aleatório, e é o tempo decorrido entre dois passos sucessivos.
Isso corresponde à função de Green da equação de difusão que controla o processo de Wiener, o que sugere que, depois de um grande número de passos, o passeio aleatório converge em direção a um processo de Wiener.
Em 3D, a variância correspondente à função de Green de difusão da equação é:
Ao equalizar essa quantidade com a variância associada à posição do caminhante aleatório, obtém-se o coeficiente de difusão equivalente a ser considerado para o processo de Wiener para qual o passeio aleatório converge depois de um grande número de passos:
- (válido apenas em 3D)
Observação: as duas expressões da variância acima correspondem à distribuição associada ao vetor que liga as duas extremidades do passeio aleatório, em 3D. A variância associada a cada componente , ou é apenas um terço deste valor (em 3D).
Para 2D:[11]
E para 1D:[12]
Passeio aleatório gaussiano[editar | editar código-fonte]
Um passeio aleatório com um passo de tamanho que varia de acordo com uma distribuição normal é usado como um modelo para séries de dados temporais do mundo real, tais como os mercados financeiros. A fórmula de Black–Scholes para a modelagem de opção de preços, por exemplo, usa um passeio aleatório gaussiano como a suposição subjacente.
Aqui, o tamanho do passo é o inverso da distribuição cumulativa normal onde 0 ≤ z ≤ 1 é uma distribuição uniforme de números aleatórios, e μ e σ são a média e o desvio-padrão da distribuição normal, respectivamente.
Se μ é diferente de zero, o passeio aleatório irá variar sobre uma tendência linear. Se vs é o valor inicial do passeio aleatório, o valor esperado depois de n passos será vs + nμ.
Para o caso especial onde μ é igual a zero, depois de n passos, a distância de translação da distribuição de probabilidade é dada por N(0, nσ2), onde N(a) é a notação para a distribuição normal, n é o número de passos, e σ é dado a partir da distribuição normal cumulativa inversa conforme indicado acima.
Prova: O passeio aleatório gaussiano pode ser considerado como a soma de uma série de independentes e identicamente distribuídas variáveis aleatórias Xi, do inverso da distribuição cumulativa normal com média igual a zero e σ da distribuição normal cumulativa inversa original:
- Z = ,
mas tem-se a distribuição para a soma de duas variáveis aleatórias independentes e normalmente distribuídas, Z = X + Y, é dada por
- N(μX + μY, σ2X + σ2Y)
No caso, µX = µY = 0 e σ2X = σ2Y = σ2 resultando em
- N(0, 2σ2)
Por indução, para n passos tem-se
- Z ~ N(0, nσ2).
Para as etapas distribuídas de acordo com qualquer distribuição, com zero de média e uma variância finita (não necessariamente apenas uma distribuição normal), o valor eficaz da distância da tradução depois de n passos é
Mas para o passeio aleatório gaussiano, este é apenas o desvio padrão da distância da tradução da distribuição depois de n passos. Portanto, se μ é igual a zero, e por que o valor eficaz (rms) da distância da tradução é um desvio-padrão, há 68.27% de probabilidade de que o rms da distância da tradução depois de n passos vai cair entre ± σ. Da mesma forma, há 50% de probabilidade de que a distância da tradução depois de n passos vai cair entre ± σ 0.6745.
Um passeio aleatório com um passo de tamanho que varia de acordo com uma distribuição normal é usado como um modelo para séries de dados temporais do mundo real, tais como os mercados financeiros. A fórmula de Black–Scholes para a modelagem de opção de preços, por exemplo, usa um passeio aleatório gaussiano como a suposição subjacente.
Aqui, o tamanho do passo é o inverso da distribuição cumulativa normal onde 0 ≤ z ≤ 1 é uma distribuição uniforme de números aleatórios, e μ e σ são a média e o desvio-padrão da distribuição normal, respectivamente.
Se μ é diferente de zero, o passeio aleatório irá variar sobre uma tendência linear. Se vs é o valor inicial do passeio aleatório, o valor esperado depois de n passos será vs + nμ.
Para o caso especial onde μ é igual a zero, depois de n passos, a distância de translação da distribuição de probabilidade é dada por N(0, nσ2), onde N(a) é a notação para a distribuição normal, n é o número de passos, e σ é dado a partir da distribuição normal cumulativa inversa conforme indicado acima.
Prova: O passeio aleatório gaussiano pode ser considerado como a soma de uma série de independentes e identicamente distribuídas variáveis aleatórias Xi, do inverso da distribuição cumulativa normal com média igual a zero e σ da distribuição normal cumulativa inversa original:
- Z = ,
mas tem-se a distribuição para a soma de duas variáveis aleatórias independentes e normalmente distribuídas, Z = X + Y, é dada por
- N(μX + μY, σ2X + σ2Y)
No caso, µX = µY = 0 e σ2X = σ2Y = σ2 resultando em
- N(0, 2σ2)
Por indução, para n passos tem-se
- Z ~ N(0, nσ2).
Para as etapas distribuídas de acordo com qualquer distribuição, com zero de média e uma variância finita (não necessariamente apenas uma distribuição normal), o valor eficaz da distância da tradução depois de n passos é
Mas para o passeio aleatório gaussiano, este é apenas o desvio padrão da distância da tradução da distribuição depois de n passos. Portanto, se μ é igual a zero, e por que o valor eficaz (rms) da distância da tradução é um desvio-padrão, há 68.27% de probabilidade de que o rms da distância da tradução depois de n passos vai cair entre ± σ. Da mesma forma, há 50% de probabilidade de que a distância da tradução depois de n passos vai cair entre ± σ 0.6745.
Movimento browniano
Movimento Browniano ou pedesis (em grego: πήδησις /pɛ̌ːdɛːsis/ "pulando") é o movimento aleatório das partículas suspensas em um fluido (líquido ou gás), resultante da sua colisão com átomos rápidos ou moléculas no gás ou líquido. O movimento Browniano é um dos mais simples processos da estocástica (ou probabilística) de tempo contínuo, e é um limite de ambos os processos mais simples e mais complicados estocásticos (veja passeio aleatório e teorema de Donsker). Esta universalidade está intimamente relacionada com a universalidade da distribuição normal. Em ambos os casos, é muitas vezes conveniência matemática, em vez da precisão dos modelos, que motiva a sua utilização.
O termo "movimento Browniano", nomeado em homenagem ao botânico Robert Brown, também pode se referir ao modelo matemático usado para descrever tais movimentos aleatórios, que muitas vezes é chamado de teoria da partícula.[1] Este modelo tem inúmeras aplicações do mundo real. Por exemplo, flutuações do mercado de ações são frequentemente citados, embora Benoît Mandelbrot rejeitou sua aplicabilidade aos movimentos de preços de ações, em parte, porque estes são descontínuos.[2]
Movimento Browniano ou pedesis (em grego: πήδησις /pɛ̌ːdɛːsis/ "pulando") é o movimento aleatório das partículas suspensas em um fluido (líquido ou gás), resultante da sua colisão com átomos rápidos ou moléculas no gás ou líquido. O movimento Browniano é um dos mais simples processos da estocástica (ou probabilística) de tempo contínuo, e é um limite de ambos os processos mais simples e mais complicados estocásticos (veja passeio aleatório e teorema de Donsker). Esta universalidade está intimamente relacionada com a universalidade da distribuição normal. Em ambos os casos, é muitas vezes conveniência matemática, em vez da precisão dos modelos, que motiva a sua utilização.
O termo "movimento Browniano", nomeado em homenagem ao botânico Robert Brown, também pode se referir ao modelo matemático usado para descrever tais movimentos aleatórios, que muitas vezes é chamado de teoria da partícula.[1] Este modelo tem inúmeras aplicações do mundo real. Por exemplo, flutuações do mercado de ações são frequentemente citados, embora Benoît Mandelbrot rejeitou sua aplicabilidade aos movimentos de preços de ações, em parte, porque estes são descontínuos.[2]
Índice
Conceito[editar | editar código-fonte]
O movimento browniano é o movimento aleatório de partículas num fluido (líquido ou gás) como consequência dos choques entre todas as moléculas ou átomos presentes no fluido. O termo movimento browniano pode ser usado para se referir a uma grande diversidade de movimentos com partículas, com moléculas, e com ambos presentes em estados desde micro até macroscópicos em situações de organização caóticas, semi-caóticas, ou de proporções matemáticas, principalmente em casos de modelagem, todos estes na área denominada Física de partículas.[1]
Esse fenômeno físico que é intrínseco à matéria e aos choques que ocorrem nos fluidos, também pode ser observado com macromoléculas, tendo por exemplo o momento que a luz incide em locais relativamente secos, permitindo que se veja macropartículas "flutuando" em suspensão no ar fazendo movimentos aleatórios. Vulgarmente confunde-se com poeira, entretanto deve-se notar que o ar (o fluido em questão) que pratica o movimento browniano e não as partículas (ou macromoléculas, neste caso poeira) que estão naquele.[1]
Há um padrão pouco explícito em alguns casos deste movimento aleatório que o classifica como um movimento fractal, pois descreve um padrão dinâmico bem definido. Quem primeiro percebeu isso foi Benoît Mandelbrot, matemático francês.
Esse movimento está diretamente ligado com muitas reações em nível celular, como a difusão, a formação de proteínas, a síntese de ATP e o transporte intracelular de moléculas.
Hoje em dia, o movimento browniano serve de modelo na descrição de flutuações que ocorrem nos mais diversos e inesperados tipos de sistemas. Por exemplo, praticamente a mesma descrição e o mesmo tratamento matemático de Einstein podem ser adaptados para descrever flutuações de preços de mercadorias, a condutividade elétrica em metais e a ocorrência de cheias nos rios.[3]
Físicos atualmente estudam tal movimento em relação à Teoria do Caos.
O movimento browniano é o movimento aleatório de partículas num fluido (líquido ou gás) como consequência dos choques entre todas as moléculas ou átomos presentes no fluido. O termo movimento browniano pode ser usado para se referir a uma grande diversidade de movimentos com partículas, com moléculas, e com ambos presentes em estados desde micro até macroscópicos em situações de organização caóticas, semi-caóticas, ou de proporções matemáticas, principalmente em casos de modelagem, todos estes na área denominada Física de partículas.[1]
Esse fenômeno físico que é intrínseco à matéria e aos choques que ocorrem nos fluidos, também pode ser observado com macromoléculas, tendo por exemplo o momento que a luz incide em locais relativamente secos, permitindo que se veja macropartículas "flutuando" em suspensão no ar fazendo movimentos aleatórios. Vulgarmente confunde-se com poeira, entretanto deve-se notar que o ar (o fluido em questão) que pratica o movimento browniano e não as partículas (ou macromoléculas, neste caso poeira) que estão naquele.[1]
Há um padrão pouco explícito em alguns casos deste movimento aleatório que o classifica como um movimento fractal, pois descreve um padrão dinâmico bem definido. Quem primeiro percebeu isso foi Benoît Mandelbrot, matemático francês.
Esse movimento está diretamente ligado com muitas reações em nível celular, como a difusão, a formação de proteínas, a síntese de ATP e o transporte intracelular de moléculas.
Hoje em dia, o movimento browniano serve de modelo na descrição de flutuações que ocorrem nos mais diversos e inesperados tipos de sistemas. Por exemplo, praticamente a mesma descrição e o mesmo tratamento matemático de Einstein podem ser adaptados para descrever flutuações de preços de mercadorias, a condutividade elétrica em metais e a ocorrência de cheias nos rios.[3]
Físicos atualmente estudam tal movimento em relação à Teoria do Caos.
Breve História[editar | editar código-fonte]
O poema didático latino De rerum natura (Sobre a natureza das coisas), escrito por Tito Lucrécio Caro cita:
-
-
-
-
-
-
- Os átomos movem-se num infinito vazio.
- O universo é composto de átomos e vazio, nada mais.
- Devido a sermos compostos de uma sopa de átomos em constante movimento[...].
- As formas de vida neste mundo e nos outros estão em constante movimento, incrementando a potência de umas formas e diminuindo a de outras.
- Os sentimentos percebem as colisões macroscópicas e interacções dos corpos[...]Albert Einstein.
Demonstrando algum conhecimento das sociedades antigas sobre como choques de partículas geram os vários fenômenos que são citados. É de se observar que na época em questão não havia aceitação e nem entendimento unânime sobre a existência de átomos e outros componentes da matéria. A disputa atômica começou com Demócrito e Anaxagoras. Os filósofos se opunham às teorias atômicas, distinguidos pela questão da gota d´água, por exemplo, que deve se dividir repetidamente sem limite, com cada subdivisão preservando as propriedades da original. A escola atômica de Demócrito defendia que as subdivisões não podiam continuar indefinidamente. A doutrina da homogeneidade seguida por Anaxagoras defende que a divisão da gota pode continuar sem término, porque o tamanho do corpo não reflete a natureza da substância.
.jpg)
O poema didático latino De rerum natura (Sobre a natureza das coisas), escrito por Tito Lucrécio Caro cita:
-
-
-
-
-
-
- Os átomos movem-se num infinito vazio.
- O universo é composto de átomos e vazio, nada mais.
- Devido a sermos compostos de uma sopa de átomos em constante movimento[...].
- As formas de vida neste mundo e nos outros estão em constante movimento, incrementando a potência de umas formas e diminuindo a de outras.
- Os sentimentos percebem as colisões macroscópicas e interacções dos corpos[...]Albert Einstein.
-
-
-
-
-
Demonstrando algum conhecimento das sociedades antigas sobre como choques de partículas geram os vários fenômenos que são citados. É de se observar que na época em questão não havia aceitação e nem entendimento unânime sobre a existência de átomos e outros componentes da matéria. A disputa atômica começou com Demócrito e Anaxagoras. Os filósofos se opunham às teorias atômicas, distinguidos pela questão da gota d´água, por exemplo, que deve se dividir repetidamente sem limite, com cada subdivisão preservando as propriedades da original. A escola atômica de Demócrito defendia que as subdivisões não podiam continuar indefinidamente. A doutrina da homogeneidade seguida por Anaxagoras defende que a divisão da gota pode continuar sem término, porque o tamanho do corpo não reflete a natureza da substância.
Descoberta do Movimento Browniano[editar | editar código-fonte]
Em 1827, ao olhar através de um microscópio partículas encontradas em grãos de pólen na água,o biólogo Robert Brown observou que as partículas se moviam através da água, mas não foi capaz de determinar os mecanismos que causaram este movimento. Assim, foi o primeiro a observar cientificamente o movimento que achou se tratar de uma nova forma de vida, pois ainda não se tinha completa ciência da existência de moléculas, e as partículas pareciam descrever movimentos por vontade própria.
Jan Ingenhousz também fez algumas observações do movimento irregular de poeira de carbono em álcool em 1765. Porém, a primeira pessoa a descrever a matemática por trás do movimento Browniano foi Thorvald N. Thiele em 1880 em um artigo no método dos menores quadrados. Isto foi seguido independentemente por Louis Bachelier em 1900 em sua tese de PhD "A Teoria da Especulação".
Átomos e moléculas , posteriormente foram teorizados como os constituintes da matéria e, muitas décadas depois, Albert Einstein publicou um artigo em 1905 que explicava em detalhes precisos como o movimento que Brown tinha observado era o resultado do pólen sendo movido por moléculas de água individuais. Esta explicação deste fenômeno de transporte serviu como a confirmação definitiva de que átomos e moléculas realmente existem, e foi ainda verificada experimentalmente por Jean Baptiste Perrin, em 1908. Perrin foi agraciado com o Prêmio Nobel de Física em 1926 "por seu trabalho sobre a estrutura descontínua da matéria" (Einstein tinha recebido o prêmio cinco anos antes "por seus serviços à física teórica", com citação específica de uma pesquisa diferente). Sendo então que a direção da força de bombardeamento atômico está constantemente mudando, e em diferentes momentos da partícula é atingido mais de um lado do que o outro, levando à natureza aparentemente aleatória do movimento.
Em 1827, ao olhar através de um microscópio partículas encontradas em grãos de pólen na água,o biólogo Robert Brown observou que as partículas se moviam através da água, mas não foi capaz de determinar os mecanismos que causaram este movimento. Assim, foi o primeiro a observar cientificamente o movimento que achou se tratar de uma nova forma de vida, pois ainda não se tinha completa ciência da existência de moléculas, e as partículas pareciam descrever movimentos por vontade própria.
Jan Ingenhousz também fez algumas observações do movimento irregular de poeira de carbono em álcool em 1765. Porém, a primeira pessoa a descrever a matemática por trás do movimento Browniano foi Thorvald N. Thiele em 1880 em um artigo no método dos menores quadrados. Isto foi seguido independentemente por Louis Bachelier em 1900 em sua tese de PhD "A Teoria da Especulação".
Átomos e moléculas , posteriormente foram teorizados como os constituintes da matéria e, muitas décadas depois, Albert Einstein publicou um artigo em 1905 que explicava em detalhes precisos como o movimento que Brown tinha observado era o resultado do pólen sendo movido por moléculas de água individuais. Esta explicação deste fenômeno de transporte serviu como a confirmação definitiva de que átomos e moléculas realmente existem, e foi ainda verificada experimentalmente por Jean Baptiste Perrin, em 1908. Perrin foi agraciado com o Prêmio Nobel de Física em 1926 "por seu trabalho sobre a estrutura descontínua da matéria" (Einstein tinha recebido o prêmio cinco anos antes "por seus serviços à física teórica", com citação específica de uma pesquisa diferente). Sendo então que a direção da força de bombardeamento atômico está constantemente mudando, e em diferentes momentos da partícula é atingido mais de um lado do que o outro, levando à natureza aparentemente aleatória do movimento.
Resultados físicos posteriores[editar | editar código-fonte]
Theodor Svedberg fez importantes demonstrações do movimento Browniano em colóides e Felix Ehrenhaft, em partículas de prata no ar.
Jean Perrin realizou experimentos para testar os novos modelos matemáticos e seus resultados publicados finalmente colocaram um fim na disputa de dois mil anos sobre a existência dos átomos e moléculas.E, por esses trabalhos, ele foi agraciado com o prêmio Nobel de Física de 1926.
Alguns anos depois do trabalho de Einstein, o matemático Norbert Wiener provou que a trajetória browniana tem comprimento infinito entre dois pontos quaisquer. O caminho traçado pela partícula é tão demorado que, se houvesse um tempo infinitamente longo, ela percorreria todo o plano, sem deixar de passar por nenhum ponto. Tecnicamente se diz que, contrariando as aparências, o caminho percorrido pela partícula browniana não é uma linha (com dimensão 1), mas é uma superfície (com dimensão 2)! E tem mais: Não pense que a trajetória da partícula browniana parece ser irregular porque o microscópio não tem um aumento suficiente para mostrar os detalhes da curva. Nada disso. Com um microscópio mais potente veríamos mais detalhes, realmente, mas a curva seria tão angulosa e irregular quanto antes[4].
Theodor Svedberg fez importantes demonstrações do movimento Browniano em colóides e Felix Ehrenhaft, em partículas de prata no ar.
Jean Perrin realizou experimentos para testar os novos modelos matemáticos e seus resultados publicados finalmente colocaram um fim na disputa de dois mil anos sobre a existência dos átomos e moléculas.E, por esses trabalhos, ele foi agraciado com o prêmio Nobel de Física de 1926.
Jean Perrin realizou experimentos para testar os novos modelos matemáticos e seus resultados publicados finalmente colocaram um fim na disputa de dois mil anos sobre a existência dos átomos e moléculas.E, por esses trabalhos, ele foi agraciado com o prêmio Nobel de Física de 1926.
Alguns anos depois do trabalho de Einstein, o matemático Norbert Wiener provou que a trajetória browniana tem comprimento infinito entre dois pontos quaisquer. O caminho traçado pela partícula é tão demorado que, se houvesse um tempo infinitamente longo, ela percorreria todo o plano, sem deixar de passar por nenhum ponto. Tecnicamente se diz que, contrariando as aparências, o caminho percorrido pela partícula browniana não é uma linha (com dimensão 1), mas é uma superfície (com dimensão 2)! E tem mais: Não pense que a trajetória da partícula browniana parece ser irregular porque o microscópio não tem um aumento suficiente para mostrar os detalhes da curva. Nada disso. Com um microscópio mais potente veríamos mais detalhes, realmente, mas a curva seria tão angulosa e irregular quanto antes[4].
Outras Pesquisas[editar | editar código-fonte]
Outro francês, Louis Bachelier, em sua tese de doutoramento apresentada em 1900, cinco anos antes do artigo de Einstein, desenvolveu praticamente toda a teoria do movimento aleatório, obtendo expressões semelhantes às que seriam depois obtidas por Einstein. No entanto, Bachelier não descrevia um sistema físico, como partículas suspensas em água, mas as flutuações das ações de uma bolsa de valores. Por essa razão, seus resultados passaram inteiramente despercebidos pelo,s físicos da época. Hoje, sabe-se que o tratamento teórico dessas flutuações serve para explicar inúmeros fenômenos que ocorrem em áreas completamente distintas, como a física, a biologia, a economia e as ciências políticas. A observação aparentemente inocente de Robert Brown revelou-se muito mais importante do que parecia do que quando foi relatada pela primeira vez. [5]
Outro francês, Louis Bachelier, em sua tese de doutoramento apresentada em 1900, cinco anos antes do artigo de Einstein, desenvolveu praticamente toda a teoria do movimento aleatório, obtendo expressões semelhantes às que seriam depois obtidas por Einstein. No entanto, Bachelier não descrevia um sistema físico, como partículas suspensas em água, mas as flutuações das ações de uma bolsa de valores. Por essa razão, seus resultados passaram inteiramente despercebidos pelo,s físicos da época. Hoje, sabe-se que o tratamento teórico dessas flutuações serve para explicar inúmeros fenômenos que ocorrem em áreas completamente distintas, como a física, a biologia, a economia e as ciências políticas. A observação aparentemente inocente de Robert Brown revelou-se muito mais importante do que parecia do que quando foi relatada pela primeira vez. [5]
Movimento Browniano na Física[editar | editar código-fonte]
A primeira teoria do Movimento Browniano na Física foi publicada por Einstein em sua tese de doutoramento no ano de 1905, publicada em "Annalen der Physik". Inicialmente, Einstein analisou as equações de Navier-Stokes para o escoamento de um fluido incompressível, obtendo:[6]
Onde,
= Viscosidade efetiva na presença de soluto;
= Viscosidade do solvente puro;
= Parte do volume total que é ocupada pelo soluto.
Assim, com base em grandezas conhecidas, como a massa molar e a densidade, tem - se que:
Desse modo, as únicas incógnitas são o raio da partícula () e o Número de Avogrado (). O cientista buscou ainda outro modo de relacionar e , obtendo um resultado matemático em que relaciona a difusão (D) com a temperatura e a viscosidade do fluido, de forma:[7]
Onde,
D = Coeficiente de Difusão
T = Temperatura Termodinâmica
= Raio das partículas
= Viscosidade do solvente puro
Por meio do Movimento Browniano, Einstein possibilitou a observação de flutuações de partículas que anteriormente possuíam desvio quadrático médio muito pequeno. A base de sua teoria é tida como a semelhança do comportamento de soluções e do comportamento de suspensões diluídas, onde existe uma relação do coeficiente de difusão com a viscosidade, somado à uma dedução probabilística da equação de difusão.[7] Diante desses cálculos, foi elaborado para o Movimento Browniano o deslocamento quadrático médio na direção "x" e o tempo de observação "t", tal que:[8]
No caso tridimensional, devido a isotropia, temos que:
Alguns anos após as descobertas de Einstein, em 1908, Paul Langevin, assim como outros cientistas, buscou a generalização das fórmulas já criadas. Assim, Langevin definiu que o Movimento Browniano de uma partícula que esteja fora de um campo de força conservativo pode ser escrito como uma equação diferencial, sendo:[9]
Onde,
= Viscosidade do meio;
= Velocidade da particula;
= Força aleatória.
Vale ressaltar que é uma força que mantêm a agitação das partículas em suspensão, sendo atribuída a força gerada pelas moléculas do fluido nas partículas suspensas.
Langevin demonstrou que a variância da velocidade é dada por:
Onde,
= Constante a ser calculada;
= Viscosidade do meio;
= Tempo.
Desse modo, para tempo longos, a função exponencial tende a zero, assim:
Levando em conta fatores como a energia cinética média das partículas, Langevin demonstra que:
Onde,
= Constante de Boltzmann;
T = Temperatura do meio externo.
Dessa maneira, para tempos suficientemente longos, a teoria de Langevin é equivalente as propostas de Einstein sobre o Movimento Browniano.
A primeira teoria do Movimento Browniano na Física foi publicada por Einstein em sua tese de doutoramento no ano de 1905, publicada em "Annalen der Physik". Inicialmente, Einstein analisou as equações de Navier-Stokes para o escoamento de um fluido incompressível, obtendo:[6]
Onde,
= Viscosidade efetiva na presença de soluto;
= Viscosidade do solvente puro;
= Parte do volume total que é ocupada pelo soluto.
Assim, com base em grandezas conhecidas, como a massa molar e a densidade, tem - se que:
Desse modo, as únicas incógnitas são o raio da partícula () e o Número de Avogrado (). O cientista buscou ainda outro modo de relacionar e , obtendo um resultado matemático em que relaciona a difusão (D) com a temperatura e a viscosidade do fluido, de forma:[7]
Onde,
D = Coeficiente de Difusão
T = Temperatura Termodinâmica
= Raio das partículas
= Viscosidade do solvente puro
Por meio do Movimento Browniano, Einstein possibilitou a observação de flutuações de partículas que anteriormente possuíam desvio quadrático médio muito pequeno. A base de sua teoria é tida como a semelhança do comportamento de soluções e do comportamento de suspensões diluídas, onde existe uma relação do coeficiente de difusão com a viscosidade, somado à uma dedução probabilística da equação de difusão.[7] Diante desses cálculos, foi elaborado para o Movimento Browniano o deslocamento quadrático médio na direção "x" e o tempo de observação "t", tal que:[8]
No caso tridimensional, devido a isotropia, temos que:
Alguns anos após as descobertas de Einstein, em 1908, Paul Langevin, assim como outros cientistas, buscou a generalização das fórmulas já criadas. Assim, Langevin definiu que o Movimento Browniano de uma partícula que esteja fora de um campo de força conservativo pode ser escrito como uma equação diferencial, sendo:[9]
Onde,
= Viscosidade do meio;
= Velocidade da particula;
= Força aleatória.
Vale ressaltar que é uma força que mantêm a agitação das partículas em suspensão, sendo atribuída a força gerada pelas moléculas do fluido nas partículas suspensas.
Langevin demonstrou que a variância da velocidade é dada por:
Onde,
= Constante a ser calculada;
= Viscosidade do meio;
= Tempo.
Desse modo, para tempo longos, a função exponencial tende a zero, assim:
Levando em conta fatores como a energia cinética média das partículas, Langevin demonstra que:
Onde,
= Constante de Boltzmann;
T = Temperatura do meio externo.
Dessa maneira, para tempos suficientemente longos, a teoria de Langevin é equivalente as propostas de Einstein sobre o Movimento Browniano.
Analogia do Marinheiro bêbado[editar | editar código-fonte]
Uma maneira simples de compreender o processo de difusão do Movimento Browniano é o passeio ao acaso em uma dimensão, que pode ser exemplificado pelo "problema do marinheiro bêbado".
Um marinheiro bêbado andando em linha reta, no eixo X, partindo de um poste dá sempre passos do mesmo tamanho. Tendo a possibilidade de caminhar para frente ou para trás. Qual será a sua distancia do poste após N passos?
Sendo a posição após n passos. temos então:
O que resulta em:
, mas
ou seja:
Sendo:
N - o número de passos dados
l - o tamanho dos passos
O Processo Lévy, no contexto da teoria das probabilidades, é um processo estocástico, ou seja, trata-se de um modelo matemático que, por meio de variáveis aleatórias, representa a evolução de um sistema de valores no tempo. Processos estocásticos são, portanto, a contraparte probabilística de um processo determinístico. No caso do processo Lévy especificamente, ele contém incrementos independentes e estacionários, ou seja, ele representa o movimento de um ponto cujos deslocamentos sucessivos são intervalos aleatórios e independentes, e estatisticamente idênticos em diferentes horários do mesmo comprimento.
Os dois exemplos mais notórios de um processo Lévy, que recebe esse nome em homenagem ao matemático francês Paul Lévy, são o movimento browniano e o processo de Poisson.
Uma maneira simples de compreender o processo de difusão do Movimento Browniano é o passeio ao acaso em uma dimensão, que pode ser exemplificado pelo "problema do marinheiro bêbado".
Um marinheiro bêbado andando em linha reta, no eixo X, partindo de um poste dá sempre passos do mesmo tamanho. Tendo a possibilidade de caminhar para frente ou para trás. Qual será a sua distancia do poste após N passos?
Sendo a posição após n passos. temos então:
O que resulta em:
, mas
ou seja:
Sendo:
N - o número de passos dados
l - o tamanho dos passos
O Processo Lévy, no contexto da teoria das probabilidades, é um processo estocástico, ou seja, trata-se de um modelo matemático que, por meio de variáveis aleatórias, representa a evolução de um sistema de valores no tempo. Processos estocásticos são, portanto, a contraparte probabilística de um processo determinístico. No caso do processo Lévy especificamente, ele contém incrementos independentes e estacionários, ou seja, ele representa o movimento de um ponto cujos deslocamentos sucessivos são intervalos aleatórios e independentes, e estatisticamente idênticos em diferentes horários do mesmo comprimento.
Os dois exemplos mais notórios de um processo Lévy, que recebe esse nome em homenagem ao matemático francês Paul Lévy, são o movimento browniano e o processo de Poisson.
Índice
Definição matemática[editar | editar código-fonte]
Um processo estocástico pode ser considerado um processo Lévy se ele satisfizer as seguintes condições:
- quase certamente
- Independência dos incrementos: Para qualquer , são independentes
- Incrementos estacionários: Para qualquer , é igual em distribuição de
- Continuidade em probabilidade: Para qualquer e que considera que
Se for um processo Lévy, então ele poderá construir uma versão de em que será quase certamente contínua à direita, limite à esquerda.
Um processo estocástico pode ser considerado um processo Lévy se ele satisfizer as seguintes condições:
- quase certamente
- Independência dos incrementos: Para qualquer , são independentes
- Incrementos estacionários: Para qualquer , é igual em distribuição de
- Continuidade em probabilidade: Para qualquer e que considera que
Se for um processo Lévy, então ele poderá construir uma versão de em que será quase certamente contínua à direita, limite à esquerda.
Propriedades[editar | editar código-fonte]
Incrementos independentes[editar | editar código-fonte]
Um processo estocástico de tempo contínuo atribui uma variável aleatória Xt para cada ponto t ≥ 0 no tempo. Com efeito, é uma função aleatória de t. Os incrementos de tal processo são as diferenças Xs − Xt entre os seus valores em momentos diferentes t < s. Chamar os incrementos de um processo independente significa que os incrementos Xs − Xt and Xu − Xv são variáveis aleatórias independentes sempre que os dois intervalos de tempo não se sobrepõem e, de modo mais genérico, qualquer número finito de incrementos atribuídos aos pares sem sobreposição de intervalos de tempo são mutuamente (não apenas pareados) independentes.
Um processo estocástico de tempo contínuo atribui uma variável aleatória Xt para cada ponto t ≥ 0 no tempo. Com efeito, é uma função aleatória de t. Os incrementos de tal processo são as diferenças Xs − Xt entre os seus valores em momentos diferentes t < s. Chamar os incrementos de um processo independente significa que os incrementos Xs − Xt and Xu − Xv são variáveis aleatórias independentes sempre que os dois intervalos de tempo não se sobrepõem e, de modo mais genérico, qualquer número finito de incrementos atribuídos aos pares sem sobreposição de intervalos de tempo são mutuamente (não apenas pareados) independentes.
Incrementos estacionários[editar | editar código-fonte]
Considerar um incremento como estacionário significa que a distribuição de probabilidade de qualquer incremento Xt − Xs depende apenas do comprimento t − s do intervalo de tempo; incrementos em intervalos de tempo longos são igualmente distribuídos de forma idêntica.
Se for um processo de Wiener, a distribuição de probabilidade de Xt − Xs é normal com valor esperado 0 e variância t − s.
Se for um processo de Poisson, a distribuição de probabilidade de Xt − Xs é uma distribuição de Poisson com valor esperado de λ (t − s), no qual λ > 0 é a "intensidade" ou "taxa" do processo.
Considerar um incremento como estacionário significa que a distribuição de probabilidade de qualquer incremento Xt − Xs depende apenas do comprimento t − s do intervalo de tempo; incrementos em intervalos de tempo longos são igualmente distribuídos de forma idêntica.
Se for um processo de Wiener, a distribuição de probabilidade de Xt − Xs é normal com valor esperado 0 e variância t − s.
Se for um processo de Poisson, a distribuição de probabilidade de Xt − Xs é uma distribuição de Poisson com valor esperado de λ (t − s), no qual λ > 0 é a "intensidade" ou "taxa" do processo.
Divisibilidade infinita[editar | editar código-fonte]
A distribuição de um processo Lévy tem a propriedade de [[divisibilidade infinita]: dado qualquer número inteiro "n", a lei relativa a um processo Lévy ao longo do tempo pode ser representada como a lei de "n variáveis randômica independentes", processo no tempo "t" pode ser representado como a lei de "n" variáveis aleatórias independentes, que são precisamente os incrementos do processo Lévy mais intervalos de tempo de comprimento t/n, que são independentes e identicamente distribuídos por hipótese. Por outro lado, para cada distribuição de probabilidade infinitamente divisível , existe um processo Lévy de tal modo que a lei de é dada por um .
A distribuição de um processo Lévy tem a propriedade de [[divisibilidade infinita]: dado qualquer número inteiro "n", a lei relativa a um processo Lévy ao longo do tempo pode ser representada como a lei de "n variáveis randômica independentes", processo no tempo "t" pode ser representado como a lei de "n" variáveis aleatórias independentes, que são precisamente os incrementos do processo Lévy mais intervalos de tempo de comprimento t/n, que são independentes e identicamente distribuídos por hipótese. Por outro lado, para cada distribuição de probabilidade infinitamente divisível , existe um processo Lévy de tal modo que a lei de é dada por um .
Momentos[editar | editar código-fonte]
Em qualquer processo Lévy com momentos finitos, o momento nth , é uma função polinomial de t; estas funções satisfazer uma identidade binomial:
Em qualquer processo Lévy com momentos finitos, o momento nth , é uma função polinomial de t; estas funções satisfazer uma identidade binomial:
Representação Lévy–Khintchine[editar | editar código-fonte]
A distribuição de um processo Lévy é caracterizada por sua função característica, que por sua vez é dada pela fórmula Lévy–Khintchine (que é geral para todas as distribuições infinitamente divisíveis):[1] Se for um processo Lévy, então sua função característica será dada por
na qual , , será a função indicadora e será a medida sigma-finite chamada de medida Lévy de , o que satisfaz a propriedade
Um processo Lévy pode conter três componentes independentes: um desvio linear, um movimento browniano e uma superposição de processos de Poisson (centralizados) independentes, com diferentes tamanhos de salto; representa a taxa de chegada (intensidade) do processo de Poisson, com salto de tamanho . Estes três componentes, e, assim, a representação Lévy–Khintchine, são totalmente determinados pelo trio Lévy–Khintchine . Especificamente, o único (não-determinístico) processo de Lévy contínuo é um movimento browniano com deriva.
A distribuição de um processo Lévy é caracterizada por sua função característica, que por sua vez é dada pela fórmula Lévy–Khintchine (que é geral para todas as distribuições infinitamente divisíveis):[1] Se for um processo Lévy, então sua função característica será dada por
![{\displaystyle \phi _{X}(\theta ):=\mathbb {E} {\Big [}e^{i\theta X}{\Big ]}=\exp {\Bigg (}ai\theta -{\frac {1}{2}}\sigma ^{2}\theta ^{2}+\int _{\mathbb {R} \backslash \{0\}}{\big (}e^{i\theta x}-1-i\theta x\mathbf {I} _{|x|<1}{\big )}\,\Pi (dx){\Bigg )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/399f9974a7971953fe34917cde92c5e7d5e0bede)
na qual , , será a função indicadora e será a medida sigma-finite chamada de medida Lévy de , o que satisfaz a propriedade
Um processo Lévy pode conter três componentes independentes: um desvio linear, um movimento browniano e uma superposição de processos de Poisson (centralizados) independentes, com diferentes tamanhos de salto; representa a taxa de chegada (intensidade) do processo de Poisson, com salto de tamanho . Estes três componentes, e, assim, a representação Lévy–Khintchine, são totalmente determinados pelo trio Lévy–Khintchine . Especificamente, o único (não-determinístico) processo de Lévy contínuo é um movimento browniano com deriva.
Nenhum comentário:
Postar um comentário